Seven segment
adalah suatu segmen-segmen yang
digunakan untuk menampilkan angka / bilangan decimal. Seven segment ini terdiri dari 7 batang LED yang disusun membentuk
angka 8 dengan menggunakan huruf a-f yang disebut DOT MATRIKS. Setiap segment
ini terdiri dari 1 atau 2 LED (Light Emitting Dioda).
Seven segment dapat menampilkan angka-angka
desimal dan beberapa karakter tertentu melalui kombinasi aktif atau tidaknya
LED penyususnan dalam seven segment. Untuk mempermudah pengguna seven segment, umumnya digunakan sebuah decoder atau sebuah seven segment driver yang akan mengatur aktif atau tidaknya led-led
dalam seven segment sesuai dengan
inputan biner yang diberikan.
Piranti
tampilan modern disusun sebagai pola 7 segmen atau dot matriks. Jenis 7 segmen
sebagaimana namanya, menggunakan pola tujuh batang led yang disusun membentuk
angka 8 seperti yang ditunjukkan pada gambar di atas. Huruf-huruf yang
diperlihatkan dalam gambar tersebut ditetapkan untuk menandai segmen-segmen
tersebut. Dengan menyalakan beberapa segmen yang sesuai, akan dapat diperagakan
digit-digit dari 0 sampai 9, dan juga bentuk huruf A sampai F (dimodifikasi).
Sinyal
input dari switches tidak dapat langsung dikirimkan ke peraga 7 segmen,
sehingga harus menggunakan decoder
BCD (Binary Code Decimal) ke 7 segmen sebagai antar muka. Decoder ini terdiri dari
gerbang-gerbang logika yang masukannya berupa digit BCD dan keluarannya berupa
saluran-saluran untuk mengemudikan tampilan 7 segmen.
Prinsip Kerja Seven Segmen
Prinsip kerja dari seven segment
ini adalah inpuan bilangan biner pada switch dikonversi masuk kedalam decoder, baru kemudian decoder mengkonversi bilangan biner
tersebut ke dalam bilangan desimal, yang mana bilangan desimal ini akan
ditampilkan pada layar seven segmen. Fungsi dari decoder sendiri adalah sebagai pengkonversi bilangan biner ke dalam
bilangan desimal.
Jenis – jenis Seven Segmen
1) Common anoda
Common anoda merupakan pin yang terhubung
dengan semua kaki anoda LED dalam seven segment. Common anoda diberi
tegangan VCC dan seven segmen dengan common
anoda akan aktif pada saat diberi logika rendah (0) atau sering disebut
aktif low. Kaki katoda dengan label a sampai h sebagai pin aktifasi yang
menentukan nyala LED.
2) Common katoda
Common katoda merupakan pin yang terhubung
dengan semua kaki katoda LED dalam seven segmen dengan common katoda akan aktif apabila diberi logika tinggi (1) atau
disebut aktif high. Kaki anoda dengan
label a sampai h sebagai pin aktifasi yang menentukan nyala LED.
Gambar 1 Jenis seven segmen common katoda dan anoda
Perangkat utama merangkai Seven Segmen Digital
Adapun perangkat utama yang digunakan untuk mrangkai modul seven segment
diantaranya adalah:
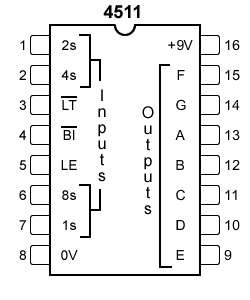
1. IC TTL 4511
Gambar 2 Datashett IC
4511
2. Seven Segment
Gambar 3 Seven
Segment
gambar 4 tabel kebenaran seven segment dengan ic 4511